dk=k-1 atau dk = k-3 untuk chi Kuadrat Dalam Uji Distribusi Normal Data

Bismillahirrahmanirrahim.

Tulisan ini mencoba memberikan uraian atas pertanyaan beberapa mahasiswa dalam seminar proposal mahasiswa IKIP Mataram hari selasa tanggal 13-03-2012 tentang derajat kebebasan distribusi chi-kuadrat untuk menguji apakah suatu data terdistribusi normal. 

Dalam berbagai referensi disebutkan bahwa, statistik   

dapat digunakan untuk menentukan kesesuaian distribusi suatu data. Khusus dalam pengujian apakah suatu data terdistribusi normal, dalam berbagai referensi statistik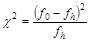  

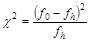
dapat diterapkan dengan dk = k-1 dan referensi yang lain menyebutkan haruslah dk=k-3.  Menjadi polemik di kalangan mahasiswa, yang benar harus menggunakan dk berapa, apakah dk = k-1 atau dk = k-3.

Berdasarkan beberapa referensi yang penulis baca, misalnya di dalam buku ilmu peluang dan statistik untuk ilmuan dan insyinyur penerbit ITB Bandung disebutkan bahwa, besarnya derajat kebebasan yang berkaitan dengan distribusi khi-kuadrat yang digunakan disini sama dengan k-1, karena hanya ada k-1 frekuensi sel yang bebas. Yaitu begitu k-1 frekuensi sel tertentu maka frekuensi sel ke k tertentu juga.  

Pernyataan ini menunjukkan bahwa "Penentuan dk = k-1 didasarkan atas pengertian dk = derajat kebebasan bahwa, jika dimiliki n buah data, maka kita hanya bebas memilih n-1 data sebagai sampel, karena data ke-n sudah sifatnya tidak bebas dipilih". 

( Sebagai contoh, misalkan dimiliki 4 buah data A, B, C dan D, maka kita bebas memilih 3 buah data secara acak, misalkan pilihan pertama B, pilihan kedua C dan pilihan ketiga A. Maka pilihan ke-4 ini sifatnya tidak bebas, karena hanya tinggal sebuah data yakni D yang sifatnya langsung di ambil tanpa dipilih).

Referensi lain, misalnya dalam dasar-dasar statistik yang ditulis Ridwan  disebutkan bahwa, dk = k-3. Lebih lanjut referensi lain menjelaskan bahwa dk = k-3 diperoleh dari (k-1)-2 yang mbermakna bahwa, terdapat k-1 ukuran sel yang bebas dipilih sebagaimana yang dijelaskan sebelumnya dan -2 dipeoleh dari kenyataan bahwa, dalam distribusi  normal terdapat 2 buah parameter yang bebas untuk ditentukan nilainya, yakni rata dan varians. Sehingga diperoleh kesimpulan bahwa, ukuran kebebasan ujinya haruslah dk = k-3.

Berdasarkan uraian di atas, kita seharusnya menggunakan yang mana dalam menguji, apakah dk = k-1 atau dk = k-3?  Jawaban penulis Wallah hu ‘Alam, karena kebenaran mutlak adalah miliknya Allah. Akan tetapi pendapat penulis ditinjau dari sisi matematika seharusnya ada kajian analitis yang menunjukkan bahwa memang dk=k-1 atau dk = k-3. 

Karena penentuan dk tersebut berdasarkan suatu pengertian saja tentunya tidak cukup, karena sifat dari suatu pengertian sangat tergantung dari sudut pandang tertentu. 

Hal ini menyebabkan pendapat seseorang bisa berbeda-beda.  Penulis akan dapat menyatakan dk = k-1 atau dk = k-3 yang benar, jika penulis sudah dapat menemukan bukti secara analitis matematika yang benar menunjukkan bahwa salah satu dari keduanya. 

Sebagaimana untuk dk dari statistik lainnya, dk = n-1 untuk , dk = n₁+n₂-2 untuk statistik  student uji beda rataan dalam kondisi varians populasi homogen yang dapat dengan jelas dibuktikan kebenarannya dengan cara analisis matematika.

Rekomendasi penulis kepada pembaca adalah, jika memegang referensi dk = k-1 dan yang menulis dalam referensi tersebut keilmuanya statistika matematikanya tidak diragukan serta tahun terbitnya terbaru, sehingga adanya keyakinan benar, gunakan dk = k-1. 

Dengan cara yang sama, jika yang dinyakini dk = k-3, maka gunakan dk = k-3. Jika ingin lebih bijaksana gunakan keduanya dan bandingkan apakah memberikan kesimpulan inferensi yang sama? 

Jika tidak sebaiknya gunakan alat uji yang lain, Karena masih banyak uji statistika yang dapat digunakan untuk menguji kenormalan suatu distribusi data. Diantaranya adalah uji Geary yang perhitungannya lebih sederhana dan sifat pengujiannya lebih kuasa dari dari uji chi-kuadrat. 

Bentuk formula matematikanya adalah

 

Formula uji Geary dapat dilihat dalam buku Ilmu peluang dan statistika untuk insyiyur dan ilmuan, penerbit ITB penulis Ronald E Walpole dan Raymond H Myers halaman 388 tentang uji kebaikan atau kesesuaian.

sumber : ripaimat.wordpress.com